Orthogonal Series' of Absolute Banach Summability

Authors

  • Pawan Saxena  
  • Madhukar Sharma  
  • Dinesh Kumar Sharma  
  • Gopal Pathak   

Keywords:

Norlund Summability, Banach Summability, Summability

Abstract

In this paper we have proved a theorem on “Orthogonal Series’of Absolute Banach Summability” which generalizes known result. However our theorem is as follows.

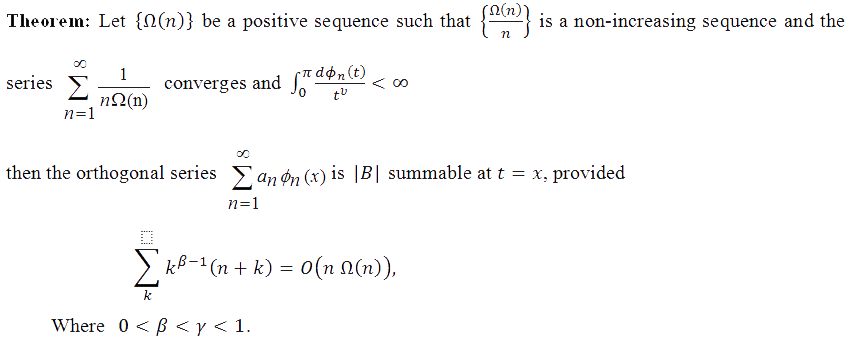
References

  1. Banach, S., Theoric dis operations Lineairs monograffe, Malematyezne, Warsaw (1932).
  2. Bosanquet, L.S. and Hyslop, J.M., On the absolute summability of the allied series of the Fourier series, Mathematics Zeitsehrift, 42(1937), 489-512.
  3. Hardy, G.H., Divergent Series, Oxford University Press, Oxford, (1949).
  4. Lal, S.N., On the Absolute Nörlund summability of Fourier Series, Indian Journal of Mathematics, 9(1967), 151-161.
  5. Leinder, L., Überstrukturbe dingungen für Fourierahen, Math, Zeitsner’s 88(1965), 418-431.
  6. Paikray,S.K., Misra,U.K. and Sahoo,N.C., Absolute banach summability of a factored Fourier series IJRRAS (2011),3-7.
  7. Okuyama, Y., On the Absolute Nörlund summability of orthogonal series, proc., Japan Academy, Vol. 54, Ser A. No. 5, (1978), 113-118.
  8. Ul’yanov, P.L., Solved and unsolved problem in the theory of trigonometric and orthogonal series, Uspehi, Math., nauk (1964), 3-69.
  9. Zygmund, A., Trigonometric series vol I and II (IInd), Cambridge University Press, Cambridge (1959).

International Journal of Scientific Research in Science, Engineering and Technology

Downloads

Published

2016-02-25

Issue

Volume 2, Issue 1, January-February-2016

Section

Research Articles

License

Copyright (c) IJSRSET

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

[1]
Pawan Saxena, Madhukar Sharma, Dinesh Kumar Sharma, Gopal Pathak , " Orthogonal Series' of Absolute Banach Summability, International Journal of Scientific Research in Science, Engineering and Technology(IJSRSET), Print ISSN : 2395-1990, Online ISSN : 2394-4099, Volume 2, Issue 1, pp.229-232, January-February-2016.